Why Students Struggle with Math (And It's Not What You Think)
Math difficulty rarely stems from inability. Research shows that 85% of math struggles come from three fixable issues: knowledge gaps from previous grades, ineffective study methods, and math anxiety.
The Three Root Causes of Math Difficulty

1. Cumulative Knowledge Gaps
Math builds on itself. If you didn't fully understand fractions in 4th grade, algebra in 9th grade becomes impossible, not because algebra is harder, but because it assumes fraction mastery.
Think of it like building a house: if the foundation has cracks, every floor above it becomes unstable.
2. Surface Level Study Habits
Most students study math by re-reading notes or watching example solutions. This creates the illusion of understanding. You recognize the process when someone shows you, but can't execute it alone.
Actual understanding requires active problem solving, not passive observation.
3. Math Anxiety and Fixed Mindset
Stanford research by Dr. Jo Boaler found that math anxiety actually impairs working memory, making problems genuinely harder to solve. Students who believe "I'm just not a math person" perform significantly worse than equally skilled peers with growth mindsets.
The anxiety isn't a symptom of being bad at math. It's often the cause.
Struggling with Math Concepts? We Can Help.
Work with academic experts who turn confusion into clarity.
- Concept based learning, not shortcuts
- Help with homework, tests, and practice
- Proven study strategies
- On time, reliable academic support
Start improving your math skills today without frustration.
Get Started NowMath vs. Other Subjects: Why Different Study Methods Matter
| Subject Type | Learning Method | Math Requirement |
|---|---|---|
| History/English | Recognition, recall | Application and creation |
| Can re-read notes | Passive review works | Active problem solving required |
| One time understanding | Read once, remember | Practice until automatic |
You can't "cram" for math the way you can for history. Math requires procedural fluency doing problems automatically, without conscious thought. This only develops through specific, deliberate practice.
8 Proven Strategies to Get Better at Math
These aren't generic "study harder" tips. Each strategy is backed by cognitive science research and used by consistently high performing math students.
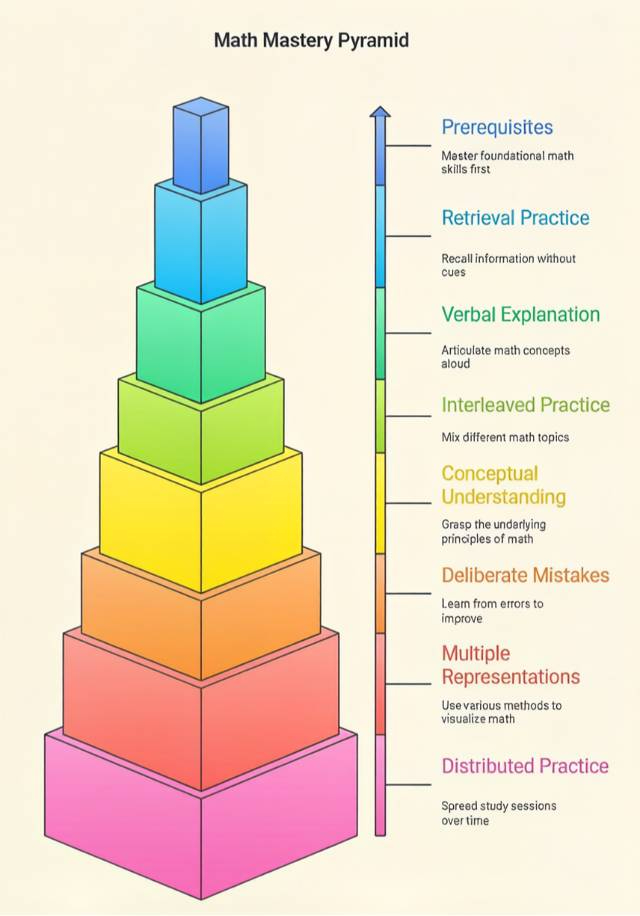
Strategy 1: Master Prerequisites Before Moving Forward
The strategy:
Identify exactly which foundational skills you're missing, then backtrack to fill those gaps before continuing.
How to implement:
- When you struggle with a problem, ask: "What prior knowledge does this assume?"
- Use Khan Academy's diagnostic test to pinpoint grade level gaps
- Spend 15–20 minutes daily reviewing prerequisite topics
- Don't move forward until you can solve 8/10 practice problems correctly
Example:
Struggling with quadratic equations? You likely have gaps in:
Fix these first. The quadratic equations will suddenly make sense. |
Research backing:
A 2023 study in Journal of Educational Psychology found students who spent 3 weeks addressing prerequisite gaps improved test scores by an average of 23 percentage points compared to students who kept pushing forward.
Strategy 2: Practice Retrieval, Not Recognition
The strategy:
Close your notes and solve problems from memory. Struggle productively before checking answers.
How to implement:
- After learning a new concept, close all materials
- Attempt 3–5 practice problems completely from memory
- If stuck, try for 2–3 minutes before checking notes
- Mark problems you couldn't solve independently
- Re attempt those problems the next day (spaced retrieval)
Why it works:
Retrieval practice strengthens neural pathways. When you struggle to recall, then succeed, your brain encodes that information more permanently than passive re-reading.
The wrong approach:
Looking at example solutions and saying "Oh yeah, I get it." This is recognition, not retrieval. You'll forget by test day.
Strategy 3: Explain Concepts Out Loud (The Feynman Technique)
The strategy:
Teach math concepts to an imaginary student or explain problems out loud as you solve them.
How to implement:
- Choose a concept you "think" you understand
- Explain it out loud in simple language (imagine teaching a 5th grader)
- Notice where you hesitate or use vague terms
- Those hesitations = gaps in your understanding
- Go back to the source material, study that specific part
- Re-explain until fluent
Example in action:
Weak explanation: "You just move the x to the other side" Strong explanation: "We're using the inverse operation to isolate x. Since 3 is being added to x, we subtract 3 from both sides to keep the equation balanced" |
Research backing:
The Feynman Technique reveals gaps that traditional studying misses. If you can't explain it simply, you don't understand it deeply.
Strategy 4: Interleave Practice (Mix Problem Types)
The strategy:
Don't do 20 problems of the same type in a row. Mix different problem types within each study session.
How to implement:
Traditional (blocked) practice:
- Problems 1–10: Solve for x in linear equations
- Problems 11–20: Factor quadratic expressions
- Problems 21–30: Graph parabolas
Interleaved practice:
- Problem 1: Linear equation
- Problem 2: Factoring
- Problem 3: Graphing
- Problem 4: Linear equation
- Problem 5: Word problem
- And so on...
Why it works:
Blocked practice feels easier but produces weaker learning. Interleaving forces your brain to identify problem types and select strategies, the exact skills needed on tests.
Research backing:
A landmark study foundthat students using interleaved practice scored 43% higher on delayed tests compared to blocked practice, despite feeling like they learned less during practice.
Strategy 5: Focus on "Why," Not Just "How"
The strategy:
For every step in a solution, ask yourself WHY that step works, not just memorize the procedure.
How to implement:
Surface approach:
"To solve 2x + 5 = 13, I subtract 5 from both sides, then divide by 2. Answer: x = 4"
Deep approach:
"I need to isolate x. Currently, x is being multiplied by 2 AND has 5 added to it. I'll undo those operations in reverse order (inverse operations). First, I subtract 5 from both sides to maintain equality: 2x = 8. Then I divide both sides by 2 to get x alone: x = 4"
| The difference: Surface learning helps you solve textbook problems that look identical to examples. Deep learning helps you solve any variation, including test problems worded differently. |
Application questions to ask:
- Why does this formula work?
- What would happen if I changed this number?
- When would I use this in real situations?
- How does this connect to previous topics?
Strategy 6: Make Mistakes Deliberately (Error Analysis)
The strategy:
Intentionally solve problems incorrectly, then analyze WHY the wrong approach fails.
How to implement:
- Solve a problem correctly first
- Now solve it using a common misconception
- Identify exactly where the flawed reasoning leads to the wrong answer
- Write a note explaining the error
Example:
Problem: Simplify (x + 3)² Common error: x² + 9 (forgetting the middle term) Error analysis: |
Why it works:
Actively analyzing errors prevents you from making them under pressure. Your brain learns to recognize warning signs.
Strategy 7: Use Multiple Representations
The strategy:
Represent every concept in at least three ways: symbolic (equations), visual (graphs/diagrams), and verbal (words).
How to implement:
For the concept "slope = rise over run":
- Symbolic: m = (y? - y?)/(x? - x?)
- Visual: Draw a line on a graph, mark two points, show the rise and run triangle
- Verbal: "Slope measures how steep a line is how much it goes up (or down) for every step right"
Why it works:
Different representations activate different brain regions. Students who use multiple representations score 30% higher on transfer problems (applying knowledge to new situations).
Application:
When studying any new topic, don't just work with equations. Draw pictures. Describe it in words. Build models if possible.
From Math Stress to Math Success.
Get professional academic assistance built around how students actually learn.
- Personalized problem-solving support
- Clear explanations in simple language
- Consistent progress tracking
- Guaranteed deadline compliance
Stop feeling stuck real improvement starts here.
Order NowStrategy 8: Schedule Distributed Practice (Spacing Effect)
The strategy:
Study math in shorter, frequent sessions spread over time rather than marathon sessions.
How to implement:
Ineffective cramming:
- Sunday: 4 hours of math before the Monday test
- Monday–Saturday: No math practice
Distributed practice:
- Daily: 30–40 minutes of math practice
- Focus each session on 2–3 concepts
- Review previous topics briefly before starting new ones
Optimal spacing schedule:
- Day 1: Learn a new concept
- Day 2: Review + practice (10 problems)
- Day 4: Review again (5 problems)
- Day 7: Final review (3 problems)
Research backing:
The spacing effect is one of the most robust findings in learning science. Distributed practice produces 200–300% better retention than massed practice.
Study Techniques Used by Top Math Students
Beyond the core strategies, high performing math students use specific study techniques that maximize efficiency.
1. The 2 Minute Rule for Problem Selection
If you can solve a problem in under 2 minutes without checking notes, you've mastered it. Stop practicing it.
Focus your limited study time on problems that take 5–10 minutes and require checking notes. These represent your growth edge.
2. Active Problem Solving Protocol
Before attempting any problem:
- Read it twice without starting
- Identify what you're solving for
- List what information you have
- Ask: "What concept does this test?"
- Now attempt the solution
After solving:
- Check your answer against the key
- If wrong, find your first error, don't just restart
- Understand WHY that step was wrong
- Redo the problem completely from memory
3. The Cornell Note Taking Method for Math
Traditional math notes are just copied examples. Cornell notes force active processing.
Format:
- Left column (30%): Key formulas, vocabulary, questions
- Right column (70%): Worked examples, explanations
- Bottom (summary): 3 sentence summary of main concepts
Application:
After class/textbook reading, cover the right column. Using only the left column cues, try to recreate the solutions from memory.
Math Study Groups Done Right
Study groups help IF structured correctly. Otherwise, they become social time.
Effective structure:
- Each person works independently first (20 min)
- Compare answers and approaches
- Discuss only problems where answers differed
- Teach each other your solution methods
- End by each person writing a summary
Warning signs your group isn't helping:
- One person explains, while others just listen
- You leave feeling goo,d but can't solve problems alone later
- More talking about the test than actually solving problems
Overcoming Math Anxiety
Math anxiety isn'ta weakness; it's a physiological response that can be addressed with specific techniques.
Understanding the Anxiety Cycle
The cycle:
- Past negative math experience = belief "I'm bad at math"
- Anxiety when facing new math problems
- Anxiety impairs working memory (makes problems genuinely harder)
- Poor performance confirms "I'm bad at math"
- Repeat
Breaking the cycle requires addressing both skills AND mindset.
Growth Mindset Interventions That Work
Research by Carol Dweck shows that short mindset interventions improve math grades by up to 25%.
Effective self talk shifts:
- "I'm not a math person" = "I haven't mastered this YET"
- "This is too hard" = "This requires different strategies"
- "I give up" = "I'll try a different approach"
| Action step: After every study session, write one specific thing you improved at, no matter how small. "Today I understood why we multiply by the reciprocal when dividing fractions" counts as progress. |
Anxiety Reduction Techniques
Before tests:
- Breathing technique: 4-7-8 breathing (inhale 4 counts, hold 7, exhale 8)
- Physical release: Tense all muscles for 10 seconds, release
- Positive visualization: Picture yourself calmly working through problems
During tests:
- Skip problems that trigger panic, do them last
- Write down formulas immediately to free working memory
- If stuck, close eyes, breathe, then approach from a different angle
Long term:
Regular practice reduces anxiety more than any technique. Familiarity builds confidence.
Common Math Mistakes That Keep Students Stuck
Avoid these traps that masquerade as effective studying.
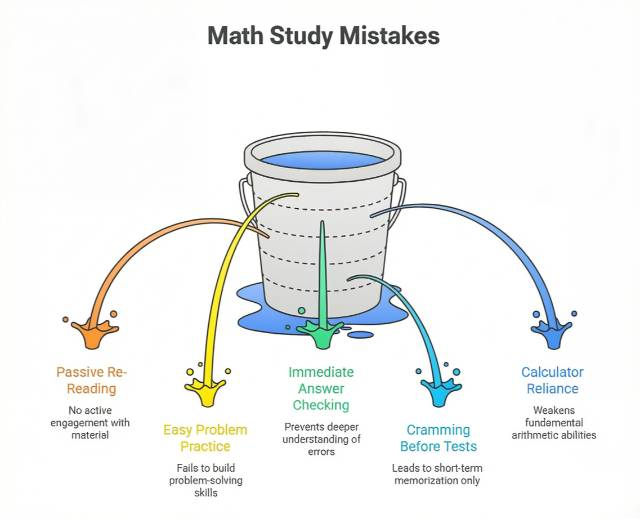
Mistake 1: Passive Re-Reading of Notes and Examples
Why it fails: Recognition ? Understanding. You feel like you know it because you recognize the solution when shown. Test day reveals you can't generate solutions independently.
Fix: Close all materials. Solve from memory. Struggle = learning.
Mistake 2: Only Practicing Easy Problems
Why it fails: You're strengthening what you already know, avoiding what you need to learn.
Fix: Spend 70% of study time on problems you get wrong initially. These are your growth opportunities.
Mistake 3: Checking Answers Immediately
Why it fails: Immediate feedback prevents productive struggle, the very thing that builds neural pathways.
Fix: Attempt 5-10 problems before checking any answers. Markthe uncertain ones. This shows you where your understanding actually ends.
Mistake 4: Studying the Night Before Tests
Why it fails: Math requires procedural memory (automatic skills). This takes days to develop, not hours.
Fix: Start test prep 7-10 days early with distributed practice sessions.
Mistake 5: Relying on Calculators for Basic Operations
Why it fails: Calculator dependency slows problem-solving and prevents you from noticing patterns.
Fix: Do basic arithmetic by hand. Use calculators only for complex operations. Build mental math fluency.
Essential Tools and Resources
Free Online Resources
- Khan Academy
Diagnostic tests identify gaps, then create personalized practice plans. Best for: filling prerequisite gaps from previous grades. - Paul's Online Math Notes
College level calculus through differential equations. Best for: clear, detailed explanations of advanced topics. - Desmos Graphing Calculator
Free online graphing tool. Best for: visualizing functions and exploring relationships. - Symbolab Step by Step Calculator
Shows detailed solution steps. Best for: checking your work and understanding where you went wrong.
Study Organization Tools
- Anki (Spaced Repetition Software)
Create flashcards for formulas and concepts. The algorithm schedules reviews at optimal intervals for retention. - Notion or OneNote
Organize notes by topic/chapter. Include links between related concepts.
For more such amazing tools, check our page of 15 best study Apps.
Struggling to apply these math study techniques on your own? Our professional essay writing service provides personalized guidance to help you implement each strategy effectively.
Your Next Steps: The 7 Day Quick Start Plan
Ready to actually get better at math? Here's your actionable first week:
Day 1-2: Take Khan Academy's diagnostic test. Identify your 3 biggest knowledge gaps. Don't move forward until you know what's missing. Day 3-4: Backtrack to fill one prerequisite gap. Use the Feynman Technique explain it out loud until fluent. Day 5-6: Practice current schoolwork using the retrieval method (notes closed). Focus on problems you get wrong. Day 7: Review the week's work using spaced repetition. Teach one concept to someone else. Then: Repeat this cycle weekly, gradually expanding to cover more concepts while maintaining distributed practice. |
Learn Math the Smart Way.
Our academic service helps you apply proven strategies the right way.
- Focus on understanding, not memorization
- Support for all math levels
- Error analysis and guided practice
- 100% original, ethical help
Turn effective study strategies into real academic results.
Get Started NowStop Struggling Start Improving
Math isn't a talent. It's a skill built through specific, strategic practice. You now have the 8 proven strategies used by top performing students, backed by cognitive science research.
The difference between students who improve and those who stay stuck? Implementation.
Don't just read this guide, use it. Pick one strategy from this article and implement it this week. Next week, add another. Small, consistent improvements compound into major grade changes.






















